Ejemplo

Sobre un grupo de n=21 personas se realizan las siguientes observaciones de sus pesos, medidos en kilogramos:

$X{\leadsto}x_1,x_2,\dots,x_{21}$

58

42

51

54

40

39

49

56

58

57

59

63

58

66

70

72

71

69

70

68

64

Agrupar los datos en una tabla estadística.

Solución:

En primer lugar hay que observar que si denominamos X a la variable ``peso de cada persona'' esta es una variable de tipo cuantitativa y continua. Por tanto a la hora de ser ordenados los resultados en una tabla estadística, esto se ha de hacer agrupándolos en intervalos de longitud conveniente. Esto nos lleva a perder cierto grado de precisión. Para que la perdida de información no sea muy relevante seguimos el criterio de utilizar  intervalos (no son demasiadas las observaciones). En este punto podemos tomar bien k=4 o bien k=5. Arbitrariamente se elige una de estas dos posibilidades. Por ejemplo, vamos a tomar k=5.

Lo siguiente es determinar la longitud de cada intervalo, ai . Lo más cómodo es tomar la misma longitud en todos los intervalos, ai=a (aunque esto no tiene por qué ser necesariamente así), donde

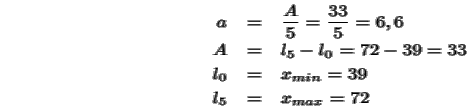
\begin{eqnarray}\html{eqn1}a&=&\frac{A}{5} = \frac{33}{5}= 6,6 \nonumber \\ A&=... ...\\ l_0&=& x_{min}= 39 \nonumber \\ l_5&=& x_{max}= 72 \nonumber \end{eqnarray}

Entonces tomaremos k=5 intervalos de longitud a=6, comenzando por l0=xmin=39 y terminando en l5=33:

 

 

Intervalos

M. clase

f.a.

f.r.

f.a.a.

f.r.a.

 

li-1 -- li

ci

ni

fi

Ni

Fi

i=1

39 -- 45,6

42,3

3

0,1428

3

0,1428

i=2

45,6 -- 52,2

48,9

2

0,0952

5

0,2381

i=3

52,2 -- 58,8

55,5

6

0,2857

11

0,5238

i=4

58,8 -- 65,4

62,1

3

0,1428

14

0,6667

i=5

65,4 -- 72

68,7

7

0,3333

21

$\approx 1$

 

21

$\approx 1$