Elección de las clases

En cuanto a la elección de las clases, deben seguirse los siguientes criterios en función del tipo de variable que se estudia:

Cuando se trate de variables cualitativas o cuasicuantitativas, las clases ci serán de tipo nominal;

$x_1,\dots,x_k$ En el caso de variables cuantitativas, existen dos posibilidades:

S ;

Si la variable es continua las clases vendrán definidas mediante lo que denominamos intervalos. En este caso, las modalidades que contiene una clase son todos los valores numéricos posibles contenidos en el intervalo, el cual viene normalmente definido de la forma

$\begin{displaymath}\left[l_{i-1} , l_{i}\right) = \left\{ x \: : \: l_{i-1} \leq x < l_i \right\} \end{displaymath}$

$\begin{displaymath}\left(l_{i-1} , l_{i}\right] = \left\{ x \: : \: l_{i-1} < x \leq l_{i} \right\} \end{displaymath}$ o bien

En estos casos se llamara amplitud del intervalo a las cantidades

y marca de clase ci, a un punto representativo del intervalo. Si éste es acotado, tomamos como marca de clase al punto más representativo, es decir al punto medio del intervalo

$\begin{displaymath}c_i = \frac{l_{i}+l_{i-1}}{2}. \end{displaymath}$

La marca de clase no es más que una forma abreviada de representar un intervalo mediante uno de sus puntos. Por ello se ha tomado como representante, el punto medio del mismo. Esto está plenamente justificado si se recuerda que cuando se mide una variable continua como el peso, la cantidad con cierto número de decimales que expresa esta medición, no es el valor exacto de la variable, sino una medida que contiene cierto margen de error, y por tanto representa a todo un intervalo del cual ella es el centro.

En el caso de variables continuas, la forma de la tabla estadística es la siguiente:

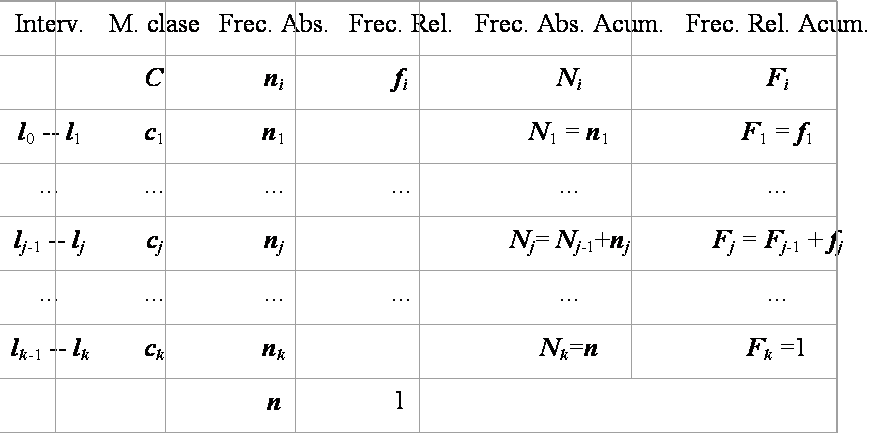
Elección de números intervalos para variables continuas

El número de intervalos, k, a utilizar no está determinado de forma fija y por tanto tomaremos un k que nos permita trabajar cómodamente y ver bien la estructura de los datos; Como referencia nosotros tomaremos una de los siguientes valores aproximados:

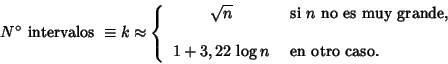
$\begin{displaymath}\mbox{$N^{\circ}$\space intervalos } \equiv k \approx \left\{... ...e 1+ 3,22 \, \log n & \mbox{ en otro caso.} \end{array}\right. \end{displaymath}$

$k=1+ 3,22 \, \log n\approx 20$ $k=\sqrt{100}=10$ Por ejemplo si el número de observaciones que se tiene es n=100, un buen criterio es agrupar las observaciones en

intervalos. Sin embargo si se tiene n=1.000.000, será mas razonable elegir intervalos, que

$k=\sqrt{1.000.000}=1.000$