---

Tal como se ha citado anteriormente, las modalidades son las diferentes situaciones posibles que puede presentar la variable. A veces éstas son muy numerosas (por ejemplo cuando una variable es continua) y conviene reducir su número, agrupándolas en una cantidad inferior de clases.

 

 

Estas clases deben ser construidas, tal como se ha citado anteriormente, de modo que sean exhaustivas e incompatibles, es decir, cada modalidad debe pertenecer a una y sólo una de las clases.

 

---

Tablas estadísticas

 

 

 

 

$c_1,c_2,\dots,c_k$Se considera una población estadística de n individuos, descrita según un carácter o variable C cuyas modalidades han sido agrupadas en un número k de clases, que se denotan mediante                            . Para cada una de las clases ci, ,

$i=1,\dots,k$                            se introduce las siguientes magnitudes:

 

---

Frecuencia absoluta

De la clase ci es el número ni, de observaciones que presentan una modalidad perteneciente a esa clase.

 

 

 

 

 

 

---

Frecuencia relativa

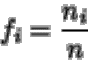\begin{displaymath}f_i = \frac{n_i}{n} \end{displaymath}De la clase ci es el cociente fi, entre las frecuencias absolutas de esta clase y el número total de observaciones, es decir

 

 

 

$100\%$
 


Se observa que fi es el tanto por uno de observaciones que están en la clase ci. Multiplicado por            representa el porcentaje de la población que comprende esa clase.

 

---

Frecuencia absoluta acumulada

 

Ni, se calcula sobre variables cuantitativas o cuasicuantitativas, y es el número de elementos de la población cuya modalidad es inferior o equivalente a la modalidad ci:

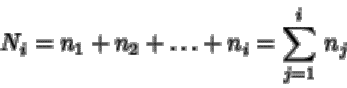
\begin{displaymath}N_i = n_1+ n_2 + \dots + n_i = \sum_{j=1}^i \, n_j \end{displaymath}
 

 

 

 

 

 

 


---

Frecuencia relativa acumulada

Fi, se calcula sobre variables cuantitativas o cuasicuantitativas, siendo el tanto por uno de los elementos de la población que están en alguna de las clases y que presentan una modalidad inferior o igual a la ci, es decir,

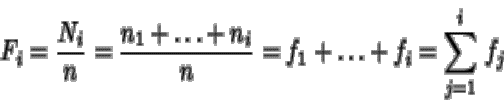
\begin{displaymath}F_i = \frac{N_i}{n} = \frac{n_1 + \dots + n_i}{n} = f_1 + \dots +f_i = \sum_{j=1}^i \, f_j \end{displaymath}
 

 

 

 

 

 

 

 

 

 


Como todas las modalidades son exhaustivas e incompatibles ha de ocurrir que

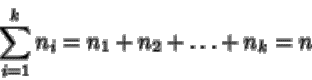
\begin{displaymath}\sum_{i=1}^k n_i = n_1 + n_2 + \dots + n_k = n \end{displaymath}
 

 

 

 

 

 

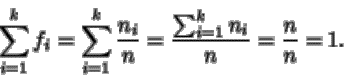
\begin{displaymath}\sum_{i=1}^k f_i = \sum_{i=1}^k \frac{n_i}{n} = \frac{\sum_{i=1}^k n_i}{n} = \frac{n}{n}=1. \end{displaymath}
 

 


o lo que es lo mismo,

 

 

---

 

Frecuencia absoluta (ni): Número de elementos que presentan

 la clase xi.

 

$\displaystyle f_i = n_i/N$
 


Frecuencia relativa:

 

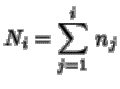
$\displaystyle N_i = \sum_{j=1}^i \, n_j$
 

 


Frecuencia absoluta acumulada:

 

 

 

  

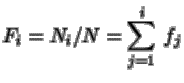
$\displaystyle F_i= N_i/N =\sum_{j=1}^i \, f_j$
 

 


Frecuencia relativa acumulada:

 

 

 

 

 

---

 

 

Se llamará distribución de frecuencias al conjunto de clases junto a las frecuencias correspondientes a cada una de ellas. Una tabla estadística sirve para presentar de forma ordenada las distribuciones de frecuencias. Su forma general es la siguiente:

 

 

 

$f_1 = \frac{n_1}{n}$,$F_1 = \frac{N_1}{n} =f_1$,$f_j = \frac{n_j}{n}$,$N_j = n_1 +\dots n_j$,$F_j = \frac{N_j}{n} =f_1 + \dots + f_j$,$f_k = \frac{n_k}{n}$
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


 

---