El contraste de Kruskall-Wallis es la alternativa no paramétrica del método ANOVA, es decir, sirve para contrastar la hipótesis de que k muestras cuantitativas han sido obtenidas de la misma población.

 La única exigencia esta sobre la aleatoriedad en la extracción de las muestras, no haciendo referencia a ninguna de las otras condiciones adicionales de homocedasticidad y normalidad necesarias para la aplicación del test paramétrico ANOVA.

De este modo, este contraste es el que se debe aplicar necesariamente cuando no se cumple algunas de las condiciones que se necesitan para aplicar dicho método.

Al igual que las demás técnicas no paramétricas, ésta se apoya en el uso de los rangos asignados a las observaciones.

Para la exposición de este contraste, supóngase que se tiene k muestras representadas en una tabla como sigue,

 

                                                                                                                                                                                   

                                                                                                                                                                         1

                                                                                                               1         2                                                          k

donde m es el número de rangos con signo de di de menor frecuencia.

Si T ó T' es menor o igual que las cantidades que aparecen en la tabla de Wilcoxon se rechaza la hipótesis nula del contraste

\begin{displaymath}\left\{ \begin{array}{l} H_0 \:\: :\:\: \mbox{No hay diferenc... ...x{\it } \\ H_1 \:\: :\:\: \mbox{Si la hay} \end{array}\right. \end{displaymath}

\begin{displaymath}N=n_1+n_2+\cdots+n_k \end{displaymath}
 

El número total de elementos en todas las muestras es:                                                            

 \begin{displaymath}\left\{ \begin{array}{l} H_0 \:\: :\:\: \mbox{Las $k$\space m... ...blación con mediana diferente a las demás} \end{array}\right. \end{displaymath}

La hipótesis a contrastar es:

El modo de realizar el contraste es el siguiente:

•Se ordenan las observaciones de menor a mayor, asignando a cada una de ellas su rango (1 para la menor, 2 para la siguiente, ...,N para la mayor).  

•Para cada una de las muestras, se calcula Ri,    , como la suma de los rangos de las observaciones que les corresponden. Si H0 es falsa, cabe esperar que esas cantidades sean muy diferentes.

Se calcula el estadístico:  

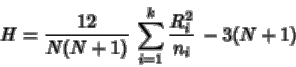\begin{displaymath}H=\frac{12}{N(N+1)} \, \sum_{i=1}^k \frac{R_i^2}{n_i} \, - 3(N+1) \end{displaymath}
 

La regla para decidir si se ha de rechazar o no la hipótesis nula es la siguiente:

•Si el número de muestras es k=3 y el número de observaciones en cada una de ellas no pasa de 5 se rechaza H0 si el valor de H supera el valor teórico que se encontra en la tabla de Kruskall-Wallis.

•En cualquier otro caso, se compara el valor de H con el de la tabla de la  con k-1 grados de libertad. Se rechaza H0 si el valor del estadístico supera el valor teórico            .