El contraste de Wilcoxon es la técnica no paramétrica paralela a el de la        de Student para muestras apareadas. Igualmente se dispondria de n parejas de valores (xi,yi) que podemos considerar como una variable medida en cada sujeto en dos momentos diferentes.

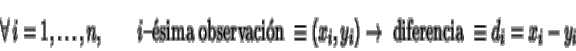
\begin{displaymath}\forall\, i=1,\dots,n,\qquad i\mbox{--ésima observación } \equiv (x_i,y_i) \rightarrow \mbox{ diferencia }\equiv d_i=x_i-y_i \end{displaymath}


El test de Wilcoxon, al igual que los otros contrastes no paramétricos puede realizarse siempre que lo sea su homólogo paramétrico, con el inconveniente de que este último detecta diferencias significativas en un    de casos que el de la       de Student.

Sin embargo a veces las hipótesis necesarias para el test paramétrico (normalidad de las diferencias apareadas, di) no se verifican y es estrictamente necesario realizar el contraste que presentamos aquí. Un caso muy claro de no normalidad es cuando los datos pertenecen a una escala ordinal.

El procedimiento consiste en:

 

1.  Ordenar las cantidades         de menor a mayor y obtener sus rangos.

2.  Considérese las diferencias di cuyo signo (positivo o negativo) tiene menor frecuencia (no se consideran las cantidades di=0) y  se calcula su suma, T

\begin{displaymath}T= \left\{ \begin{array}{l} \sum_{d_i>0}\, i \qquad \mbox{si ... ...s negativos de $d_i$ son menos frecuentes.} \end{array}\right. \end{displaymath}
 

Del mismo modo es necesario calcular la cantidad T', suma de los rangos de las observaciones con signo de di de mayor frecuencia, pero si se ha ya calculado T la siguiente expresión de T' es más sencilla de usar    

T' = m(n+1)-T

Aproximación normal en el contraste de Wilcoxon

Si   la distribución de T admite una aproximación normal.

\begin{displaymath}T{\: \stackrel{\approx}{\leadsto}\:}{ {{\bf N} \left( \mu_T,\sigma_T^2 \right)} } \end{displaymath}

 

 

donde
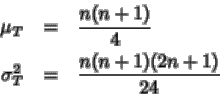
\begin{eqnarray*}\mu_T&=& \frac{n(n+1)}{4} \\ \sigma_T^2&=& \frac{n (n+1)(2n+1)}{24} \end{eqnarray*}

por lo que el estadístico

\begin{displaymath}Z=\frac{T-\mu_T}{\sigma_T} {\: \stackrel{\approx}{\leadsto}\:}{ {{\bf N} \left( 0,1 \right)} } \end{displaymath}
 

 

resulta como criterio el rechazar H0 si $\left\vert Z\right\vert\geq z_{1-\alpha/2}$