Contraste de Mann--Withney

Contraste de Mann—Withney

El objetivo es el mismo que el del test anterior: contrastar la hipótesis

$\begin{displaymath}\left\{ \begin{array}{l} H_0 \:\: :\:\: \mbox{Las poblaciones... ...{Las poblaciones no están equidistribuidas} \end{array}\right. \end{displaymath}$

para dos muestras , cuantitativas independientes, tomadas de modo aleatorio. El contraste se efectúa combinando las dos muestras y disponiendo el conjunto completo de las observaciones, ordenado de menor a mayor. Se asignan después números de rango a cada observación

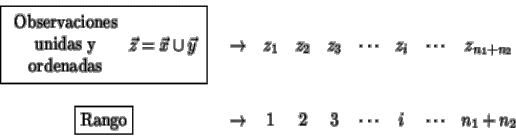
$\begin{displaymath}\begin{array}{ccccccccc} \mbox{\fbox{$ \begin{array}{c} \mb... ...htarrow & 1 & 2 & 3 & \cdots & i & \cdots & n_1+n_2 \end{array}\end{displaymath}$

Se calcula después la suma de los rangos de las observaciones pertenecientes a la primera muestra y a la segunda, obteniéndose respectivamente R1 y R2, para después calcular los estadísticos

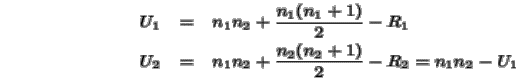
$\begin{eqnarray}\html{eqn2}U_1 &=& n_1 n_2 + \frac{n_1(n_1+1)}{2} -R_1 \\ U_2 &=& n_1 n_2 + \frac{n_2(n_2+1)}{2} -R_2 = n_1 n_2 - U_1 \end{eqnarray}$

Entonces si la hipótesis H0 es cierta, U1 y U2tienen una distribución de Mann--Withney de parámetros n1 y n2que está tabulada para valores en que

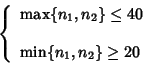
$\begin{displaymath}\left\{ \begin{array}{l} \max\{n_1,n_2\}\leq 40 \\ \\ \min\{n_1,n_2\}\geq 20 \end{array}\right. \end{displaymath}$

$\begin{displaymath}U_{exp}=\min\{U_1,U_2\} \end{displaymath}$

Para el contrate bilateral, se define

$U_{exp} < U_{n_1,n_2,\alpha}$ y se rechaza H0 si

Si el contraste que pretendemos realizar es unilateral, como por ejemplo,

$\begin{displaymath}\left\{ \begin{array}{l} H_0 \:\: :\:\: \mbox{La primera pobl... ... :\:\: \mbox{Los de la segunda son menores} \end{array}\right. \end{displaymath}$

rechazaremos la hipótesis nula si Si el test es el contrario

$\begin{displaymath}\left\{ \begin{array}{l} H_0 \:\: :\:\: \mbox{La segunda pobl... ... :\:\: \mbox{Los de la primera son menores} \end{array}\right. \end{displaymath}$

$U_1<U_{n_1,n_2,\alpha}$ se rechaza H0

Aproximación normal del test de Mann—Withney

Cuando los tamaños de las muestras son grandes, n1,n2>40, no es posible recurrir a las tablas de Mann--Withney. En este caso se utiliza la aproximación normal.

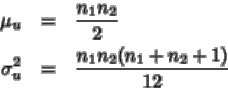$\begin{eqnarray*}\mu_u&=&\frac{n_1 n_2}{2} \\ \sigma_u^2&=& \frac{ n_1 n_2 (n_1+n_2+1)}{12} \end{eqnarray*}$ donde

y se utiliza el estadístico de contraste

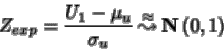
$\begin{displaymath}Z_{exp}=\frac{U_1-\mu_u}{\sigma_u} {\: \stackrel{\approx}{\leadsto}\:}{ {{\bf N} \left( 0,1 \right)} } \end{displaymath}$

rechazándose la misma distribución de ambas poblaciones utilizando los mismos criterios que con los contrastes paramétricos