![]()
las dos muestras estén muy
entremezcladas, y por tanto el número de rachas, ![]() ,formadas por las categorías
,formadas por las categorías
Contraste de rachas de Wald—Wolfowitz
![]()
las dos muestras estén muy
entremezcladas, y por tanto el número de rachas, ![]() ,formadas por las categorías
,formadas por las categorías
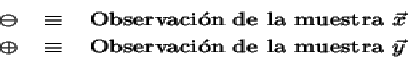
debe
ser muy alto
Cuando ![]() el valor teórico del número de rachas por debajo del
cual se rechaza ,
el valor teórico del número de rachas por debajo del
cual se rechaza , ![]()
se busca en la tabla especifica y entonces no se rechaza si
Si
n1>30 o bien n2>30 se aproxima R por
donde
se
rechaza la hipótesis nula si
Si se tiene observaciones
repetidas en las dos muestras se fija el criterio de colocar primero aquellas
que pertenecen a la primera muestra.
![]()
![]() y se rechaza en otro caso.
y se rechaza en otro caso.
![]()
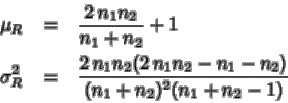
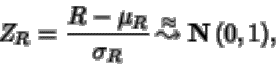 Luego si se
define
Luego si se
define
![]()
![]()