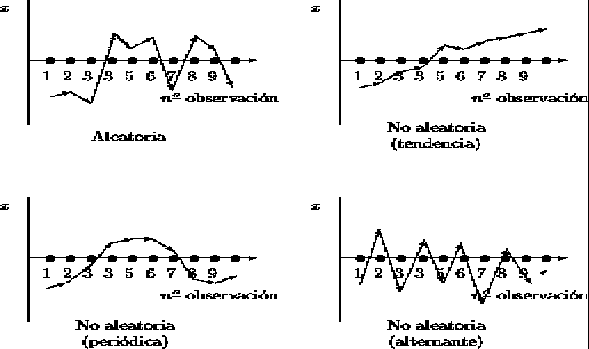
A veces al realizar un muestreo, puede llegar a influir el orden temporal o
espacial en que las muestras han sido elegidas, con lo cual no se esta en las
condiciones de un muestreo aleatorio simple, ya que la ley de probabilidad varía
de una observación a otra.
Como se observa la figura 1.1. También se puede denominar a este
contraste como test de independencia de las observaciones de una muestra.
Se considera una
muestra de tamaño n que ha sido dividida en dos categorías A y B con n1 y
n2 observaciones cada una. Se denomina racha a una sucesión de valores de la
misma categoría. Por ejemplo si se estudia una población de personas se puede
considerar como categoría el sexo
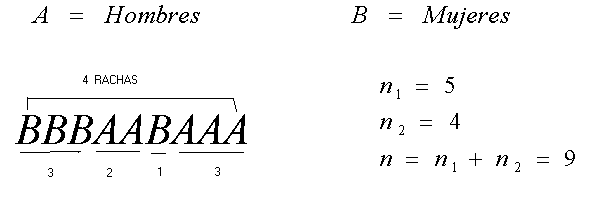En función de las cantidades n1 y n2 se espera
que el número de rachas no sea ni muy pequeño ni muy grande.
Si
las observaciones son cantidades numéricas estas pueden ser divididas en dos
categorías que poseen aproximadamente el mismo tamaño
si consideramos la mediana de las observaciones como el valor que
sirve para dividir a la muestra:
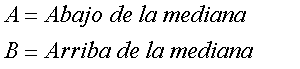Se define la variable aleatoria R como el número de rachas. Su
distribución está tabulada para los casos
(Distribución
del número total de Rachas ). La aleatoriedad en la extracción de la muestra se rechaza cuando
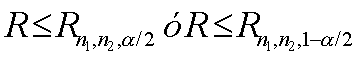Aproximación normal del test de
rachas
Si
el tamaño de cualquiera de las dos muestras es mayor que 30, la distribución
de R se aproxima a una normal de media
y
varianza
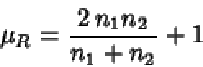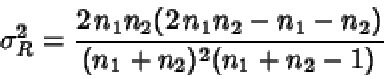y se considera el estadístico
Se
rechaza la hipótesis nula (aleatoriedad) si .
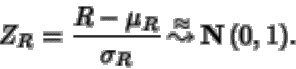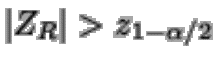Normalidad de una muestra: Test de D'Agostino
Considérese
n observaciones, las cuales ordenamos de menor a mayor y se le asigna su
rango en función de este orden
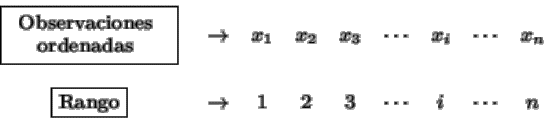Se
calculan sobre la muestra la media, la desviación típica un estadístico
T y por último el estadístico del contraste D cuya distribución está tabulada
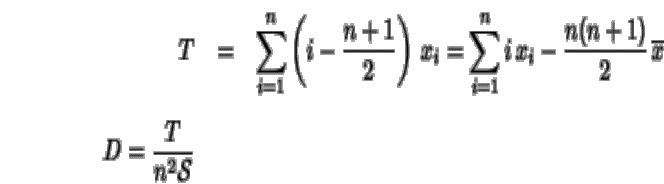En la tabla de la distribución del estadístico
de D'Agostino, D, para un nivel de significación
, se busca un intervalo
se rechaza la normalidad
y en otro caso se asume. Para realizar este prueba es necesario que al menos
