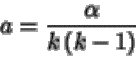
En aquellas situaciones en las que se haya rechazado la hipótesis acerca de la igualdad de las distribuciones poblacionales de las cuales hayan sido extraídas las muestras, será necesario, igual que en el caso del ANOVA, realizar contrastes a posteriori que determinen o precisen entre qué muestras existen las diferencias significativas que provocan el rechazar la hipótesis nula del contraste de Kruskal-Wallis.  

El procedimiento consistirá en los siguientes pasos:

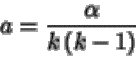\begin{displaymath}a=\frac{\alpha}{k \, (k-1)} \end{displaymath}
 

 

En primer lugar en determinar la cantidad:                

Posteriormente se calcula el valor del percentil de la distribución     N(0,1) , z1-a.

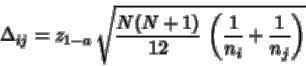\begin{displaymath}\Delta_{ij}= z_{1-a}\, \sqrt{ \displaystyle \frac{N(N+1)}{12}\, \left(\frac{1}{n_i} + \frac{1}{n_j}\right) } \end{displaymath}
 

•Por último se calcula la cantidad     

\begin{displaymath}\left\vert \overline{R}_i- \overline{R}_j \right\vert > \Delta_{ij} \end{displaymath}

                               

y en lo que respecta a la regla de decisión se dirá que existen diferencias significativas entre dos poblaciones siempre que:                   
\begin{displaymath}\overline{R}_i = \frac{R_i}{n_i} \end{displaymath}

donde es el rango medio de la muestra i, es decir,

           

no admitiendo posibles diferencias en otro caso.