---

ESTADÍSTICOS DE POSICIÓN

---

Para una variable discreta, se define el percentil de orden k, como la observación, Pk, que deja por debajo de si el  k%  de la población. Esta definición nos recuerda a la mediana, pues como consecuencia de la definición es evidente que

 

Med= P50


En el caso de una variable continua, el intervalo donde se encuentra , se calcula buscando el que deja debajo de si al  k% de las observaciones. Dentro de él, Pk se obtiene según la relación:

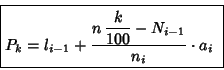
\begin{displaymath}{ \mbox{\fbox{$\displaystyle P_k = l_{i-1} + \frac{ \displaystyle n\, \frac{k}{100} - N_{i-1}}{n_i} \cdot a_i $ } } } \end{displaymath} 

---

Los cuartiles, Ql, son un caso particular de los percentiles. Hay 3, y se definen como:

\begin{eqnarray}\html{eqn7}Q_1 &=& P_{25} \\ Q_2 &=& P_{50} \qquad = {M_{ed}} \\ Q_{3} &=& P_{75} \end{eqnarray}


---

De forma análoga se definen los deciles como los valores de la variable que dividen a las observaciones en 10 grupos de igual tamaño. Más precisamente, definimos D1,D2, ..., D9 como:

 

\begin{displaymath}D_i = P_{10\,i} \qquad i=1,\, \dots, \, 9 \end{displaymath}


Los percentiles (que incluyen a la mediana, cuartiles y deciles) también son denominados estadísticos de posición.

---

Ejemplo

Dada la siguiente distribución en el número de hijos de cien familias, calcular sus cuartiles.

xi

ni

Ni

0

14

14

1

10

24

2

15

39

3

26

65

4

20

85

5

15

100

 

n=100

 
---

Solución:

1.

Primer cuartil:

 

\begin{displaymath}\displaystyle \frac{n}{4} =25; \mbox{ Primera }N_i>n/4 = 39; \mbox{ luego } {\cal Q}_1=2. \end{displaymath}


2.

Segundo cuartil:

 

\begin{displaymath}\displaystyle \frac{2\, n}{4} =50; \mbox{ Primera }N_i>2\,n/4 = 65 ; \mbox { luego } {\cal Q}_2=3. \end{displaymath}


3.

Tercer cuartil:

 

\begin{displaymath}\displaystyle \frac{3\, n}{4} =75; \mbox{ Primera }N_i>3\,n/4 = 85; \mbox{ luego }{\cal Q}_3=4. \end{displaymath}


---

Ejemplo

 

Calcular los cuartiles en la siguiente distribución de una variable continua:

li-1 - li

ni

Ni

0 - 1

10

10

1 - 2

12

22

2 - 3

12

34

3 - 4

10

44

4 - 5

7

51

 

n=51

 

 

---

Solución:

1.

Primer cuartil

 

\begin{displaymath}\frac{N}{4}=12,75; \mbox{ Primera }N_i>n/4=22; \mbox{ La línea $i$\space es la del intervalo }[1;2) \end{displaymath}


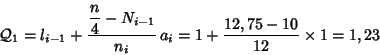
\begin{displaymath}{\cal Q}_1=l_{i-1}+ \frac{\displaystyle \frac{n}{4} - N_{i-1}}{n_i}\,a_i = 1+\frac{12,75-10}{12}\times 1 = 1,23 \end{displaymath}

 

---


2.

Segundo cuartil:

\begin{displaymath}\frac{2\, n}{4}=25,5; \mbox{ Primera }N_i>2\,n/4=34; \mbox{ La línea $i$\space es la del intervalo }[2;3) \end{displaymath}


 

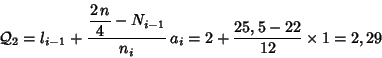
\begin{displaymath}{\cal Q}_2=l_{i-1}+ \frac{\displaystyle \frac{2\,n}{4} - N_{i-1}}{n_i}\,a_i = 2+\frac{25,5-22}{12}\times 1 = 2,29 \end{displaymath}


---

3.

Tercer cuartil

\begin{displaymath}\frac{3\,n}{4}=38,25; \mbox{ Primera }N_i>3\,n/4=44; \mbox{ La línea $i$\space es la del intervalo }[3;4) \end{displaymath}


 

\begin{displaymath}{\cal Q}_3=l_{i-1}+ \frac{\displaystyle \frac{3\,n}{4} - N_{i-1}}{n_i}\,a_i = 3+\frac{38,25-34}{10}\times 1 = 3,445 \end{displaymath}


---