---

LA MEDIANA

---

Consideramos una variable discreta X cuyas observaciones en una tabla estadística han sido ordenadas de menor a mayor. Llamaremos mediana, Medal primer valor de la variable que deja por debajo de sí al de las observaciones. Por tanto, si n es el número de observaciones, la mediana corresponderá a la observación [n/2]+1.

---

En el caso de variables continuas, las clases vienen dadas por intervalos, y aquí la fórmula de la mediana se complica un poco más (pero no demasiado): Sea (li-1,li] el intervalo donde hemos encontrado que por debajo están el de las observaciones. Entonces se obtiene la mediana a partir de las frecuencias absolutas acumuladas, mediante la expresión

 

 

 

---

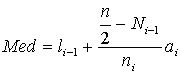
Observación

 

Entre las propiedades de la mediana, vamos a destacar las siguientes:

*  Como medida descriptiva, tiene la ventaja de no estar afectada por las observaciones extremas, ya que no depende de los valores que toma la variable, sino del orden de las mismas. Por ello es adecuado su uso en distribuciones asimétricas.

*  Es de cálculo rápido y de interpretación sencilla.

*  A diferencia de la media, la mediana de una variable discreta es siempre un valor de la variable que estudiamos (ej. La mediana de una variable número de hijos toma siempre valores enteros).

*  El mayor defecto de la mediana es que tiene unas propiedades matemáticas complicadas, lo que hace que sea muy difícil de utilizar en inferencia estadística.

*  Es función de los intervalos escogidos.

*  Puede ser calculada aunque el intervalo inferior o el superior no tenga límites.


---

Ejemplo

Sea X una variable discreta que ha presentado sobre una muestra las modalidades

\begin{displaymath}X \leadsto 2,5,7,9,12 \Longrightarrow \overline{x}=7, \qquad {M_{ed}}= 7 \end{displaymath}


Si cambiamos la última observación por otra anormalmente grande, esto no afecta a la mediana, pero si a la media:

\begin{displaymath}X \leadsto 2,5,7,9,125 \Longrightarrow \overline{x}= 29,6; \qquad {M_{ed}}= 7 \end{displaymath}


En este caso la media no es un posible valor de la variable (discreta), y se ha visto muy afectada por la observación extrema. Este no ha sido el caso para la mediana.

 

---

Ejemplo

Obtener la media aritmética y la mediana en la distribución adjunta. Determinar gráficamente cuál de los dos promedios es más significativo.

li-1 - li

ni

0 - 10

60

10 - 20

80

20 - 30

30

30 - 100

20

100 - 500

10

Solución:

li-1 - li

ni

ai

xi

xi ni

Ni

$n_i{\mbox{$'$ }}$

0 - 10

60

10

5

300

60

60

10 - 20

80

10

15

1.200

140

80

20 - 30

30

10

25

750

170

30

30 - 100

20

70

65

1.300

190

2,9

100 - 500

10

400

300

3.000

200

0,25

 

n=200

 

 

$\sum x_i n_i=6.550$

 

 

La media aritmética es:

 

\begin{displaymath}\overline{x}=\frac{1}{n}\sum x_i = \frac{6.550}{200}=32,75 \end{displaymath}


La primera frecuencia absoluta acumulada que supera el valor n/2=100 es Ni=140. Por ello el intervalo mediano es [10;20). Así:

 

\begin{displaymath}{M_{ed}}=l_{i-1}+\frac{n/2-N_{i-1}}{n_i}\cdot a_i = 10 +\frac{100-60}{80}\times 10 = 15 \end{displaymath}

 

---