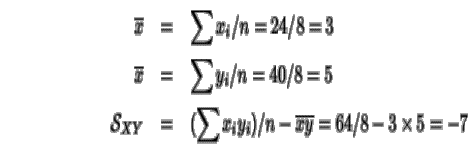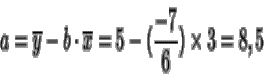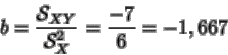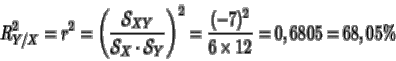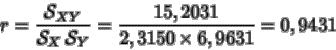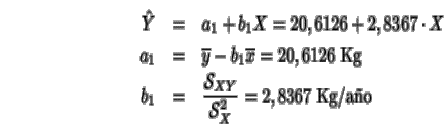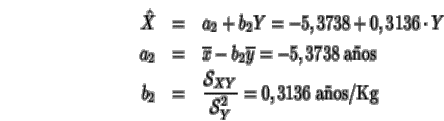Problema 1
De una muestra de ocho observaciones conjuntas de valores de dos variables X e Y , se obtiene la siguiente información:
 |
 |
Calcular:
1. La recta de regresión de Y sobre X . Explique el significado de los parámetros.
2. El coeficiente de determinación. Comente el resultado e indique el tanto por ciento de la variación de Y que no está explicada por el modelo lineal de regresión.
Si
el modelo es adecuado, ¿cuál es la predicción
para x=4 ?
Solución:
En primer lugar se calcula las medias y las covarianza entre ambas variables:
 |
Con estas cantidades se puede determinar los parámetros a y b de la recta. La pendiente de la misma es b , y mide la variación de cuando X en una unidad:
 |
 |
Al ser esta cantidad negativa, tenemos que la pendiente de la recta es negativa, es decir, a medida que X aumenta, la tendencia es a la disminución de Y. En cuanto al valor de la ordenada en el origen, a , se tiene:
Así, la recta de regresión de Y como función de es: X
 |
2.El grado de bondad del ajuste se obtiene a partir del coeficiente de determinación:
 |
Es decir, el modelo de regresión lineal explica el 68 % de la variabilidad de Y en función de la de X . Por tanto queda un 32 % de variabilidad no explicada.
3. La predicción que realiza el modelo
lineal de regresión x=4 para
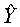es:
 |
la cual hay que considerar con ciertas reservas, pues como hemos visto en el apartado anterior, hay una razonable cantidad de variabilidad que no es explicada por el modelo.
Problema 2
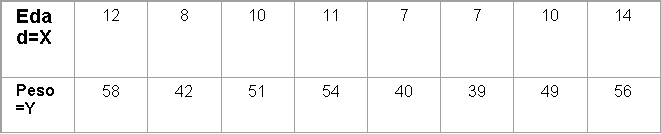
En un grupo de 8 pacientes se miden las cantidades antropométricas peso y edad, obteniéndose los siguientes resultados:
Resultado de las Mediciones
 |
¿Existe una relación lineal importante entre ambas variables?
Calcular la recta de regresión de la edad en función del peso y la del peso en función de la edad.
Calcular la bondad del ajuste ¿En qué medida, por término medio, varía el peso cada año? ¿En cuánto aumenta la edad por cada kilo de peso?
Solución:
Para saber si existe una relación lineal entre ambas variables se calcula el coeficiente de correlación lineal, que vale:
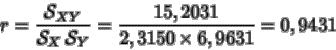
ya que
Por tanto el ajuste lineal es muy bueno. Se puede decir
que el ángulo entre el vector formado por las desviaciones del peso con
respecto a su valor medio y el de la edad con respecto a
su valor medio,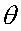 
, es:
 |
es decir, entre esos vectores hay un buen grado de paralelismo (sólo unos 19 grados de desviación).
La recta de regresión del peso en función de la edad es
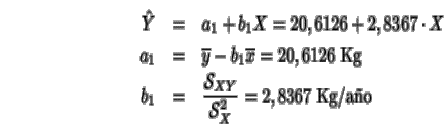
La recta de regresión de la edad como función del peso es
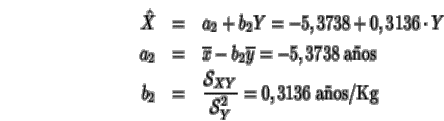
La bondad del ajuste es 
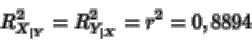
Por lo tanto se dice que el 88.94 % de la variabilidad del peso en función de la edad es explicada mediante la recta de regresión correspondiente. Lo mismo podemos decir en cuanto a la variabilidad de la edad en función del peso. Del mismo modo puede decirse que hay un 100 - 88.94 %=11.06 % de varianza que no es explicada por las rectas de regresión. Por tanto la varianza residual de la regresión del peso en función de la edad es
 |
la de la edad en función del peso:
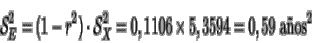
Por último la cantidad en que varía el peso de un paciente cada año es, según la recta de regresión del peso en función de la edad, la pendiente de esta recta, es decir, b1 =2,8367 Kg/año. Cuando dos personas difieren en peso, en promedio la diferencia de edad entre ambas se rige por la cantidad
b2 = 0,3136 años/Kg de diferencia.
|
