En este punto hay que evaluar si realmente esta predicción puede considerarse confiable. Para dar una respuesta, es necesario estudiar propiedades de la  regresión lineal que están a continuación.

Una vez que ya se tiene definida , (o bien   ) es necesario saber que  relación  hay entre la media y la varianza de esta y la de  Y  (o la de  X ).

La respuesta se encuentra en la siguiente proposición:

En los ajustes lineales se conservan las medias, es decir

En cuanto a la varianza, no necesariamente son las mismas para los verdaderos valores de las variables      X  e   Y   y sus aproximaciones     y   , pues sólo se mantienen en un factor de       , es decir

 

Basta probar la afirmación para la variable  Y , ya que para  X  es totalmente análogo:

 

 

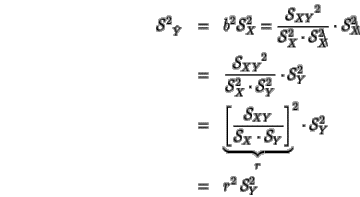donde se ha utilizado la magnitud que se denomina coeficiente de correlación, y que ya se definió anteriormente como

 

Nota

Como consecuencia de este resultado, se puede decir que la proporción de varianza explicada por la regresión lineal es del 

Lo deseable seria tener que  r=1 , pues en ese caso ambas variables tendrían la misma varianza, pero esto no es cierto en general. Todo lo que se puede afirmar,  es que

y por tanto

 

La cantidad que le falta a la varianza de regresión, , para llegar hasta la varianza total de  Y  ,      , es lo que se denomina varianza residual,     que no es más que la varianza de Y , ya que

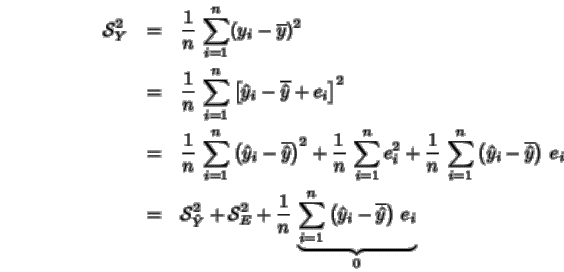El tercer sumando se anula, como se presenta mas adelante:

 

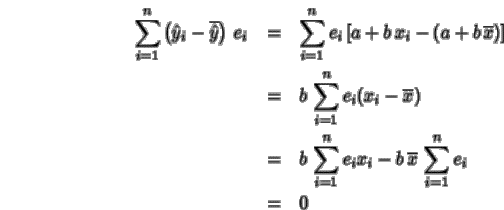Por ello

 

Obsérvese que entonces la bondad del ajuste es

 

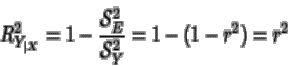
Para el ajuste contrario se define el error como , y su varianza residual es también proporcional a  1-r²

 

y el coeficiente de determinación (que sirve para determinar la bondad del ajuste de      en función de      ) es:

 

lo cual  se resume en la siguiente proposición:

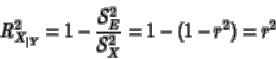
Proposición

Para los ajustes de tipo lineal se tiene que los dos coeficientes de determinación son iguales a   r² , y por tanto representan además la proporción de varianza explicada por la regresión lineal:

Por ello:

     Si   el ajuste es bueno (  Y se puede calcular de modo bastante aproximado a partir de   X    y  viceversa).

     Si  las variables  X  e  Y  no están relacionadas (linealmente al menos), por tanto no tiene sentido hacer un ajuste lineal. Sin embargo no es seguro que las dos variables no posean ninguna relación en el caso       ya que si bien el ajuste lineal puede no ser no adecuado, tal vez otro tipo de ajuste sí lo sea.