Regresión de X sobre Y

Las mismas conclusiones se obtienen cuando se  hace la regresión de  X   sobre   Y,   pero  para calcular la recta de regresión de   X   sobre   Y   es  totalmente incorrecto despejar de: 

Pues esto  da la regresión de      sobre   Y  , que no es lo que se busca . La regresión de   X  sobre   Y  se hace aproximando  X    por      , de tal forma que:

donde

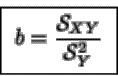de este modo se minimiza, en el sentido de los mínimos cuadrados, los errores entre las cantidades   X_i    y las    (figura 1.4.)

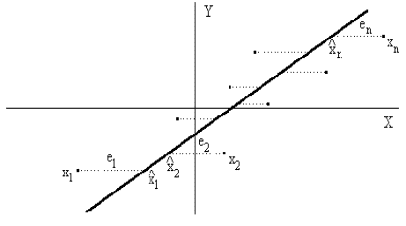
Figura 1.4 :Los errores a minimizar son las cantidades

Ejemplo

En una muestra de 1500 individuos se recogen datos sobre dos medidas antropométricas X e Y. Los resultados se muestran resumidos en los siguientes  estadísticos:

 

Obtener el modelo de regresión lineal que mejor aproxima Y en función de X . Utilizando este modelo, calcular de modo aproximado la cantidad  Y  esperada cuando  X=15 .

Solución:

Lo que se busca es la recta,   ,que mejor aproxima los valores de   Y  (según el criterio de los mínimos cuadrados) en la nube de puntos que resulta de representar en un plano (X,Y) las 1500 observaciones. Los coeficientes de esta recta son:

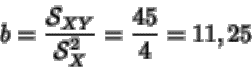Así, el modelo lineal consiste en:

 

Por tanto, si  X=15   el modelo lineal predice un valor de Y de: