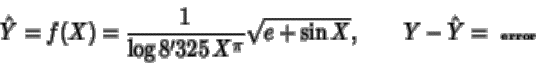 |
La forma de la función f en principio podría ser arbitraria, y tal vez se tenga que la relación más exacta entre las variables peso y altura definidas anteriormente sea algo de la forma
|
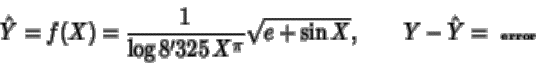Por el momento no se pretende encontrar relaciones tan complicadas entre variables, por lo cual se limitará al caso de la regresión lineal. Con este tipo de regresiones se puede encontrar relaciones funcionales de tipo lineal, es decir se buscan las cantidades a y b tales que se pueda escribir
 |
con el menor error posible entre 
e Y, o bien
 |
de forma que 
sea
una variable que toma valores próximos a cero.
Nota
Obsérvese que la relación
explica
cosas como que si X varía en 1 unidad, 
varía la cantidad
b. Por tanto:
Si b>0 , las dos variables aumentan o disminuyen a la vez;
Si b<0 , cuando una variable aumenta, la otra disminuye.
Por lo tanto, en el caso de las variables peso y altura lo lógico será encontrar que b>0
El problema que se plantea es entonces el de cómo calcular las cantidades a y b a partir de un conjunto de n observaciones
 |
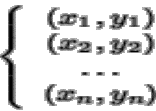de forma que se minimice el error. Las etapas en que se divide el proceso que va ha desarrollar son de forma esquemática, las siguientes:
1.Dadas dos variables X , Y , sobre las que se define
 |
se mide el error que
se comete al aproximar Y mediante 
calculando
una suma de las diferencias entre los valores reales
y los aproximados al cuadrado (para que sean positivas y no se compensen los
errores):
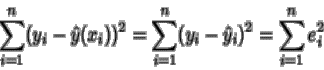
2. Una aproximación 
de
Y , se define a partir de dos cantidades a y
b . Se calculará aquellas que minimizan la función
 |
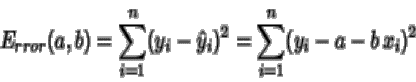3. Posteriormente se encuentran las fórmulas para el cálculo directo de Y que servirán para cualquier problema.
