Las técnicas de regresión permiten hacer predicciones sobre los valores de cierta variable Y (dependiente), a partir de los de otra X (independiente), entre las que se supone que existe una relación. Para mejor comprensión de  este concepto, se vera el siguiente ejemplo:

Altura medida en  centímetros

Altura medida en  metros

No es cierto que conocida la altura  de un individuo, se puede determinar de modo exacto su peso        (por ejemplo. dos personas que miden 1,70 m pueden tener pesos que varíen entre  60 y 65 kilos). Sin embargo, alguna relación entre ellas debe existir, parece mucho más probable que un individuo de 2 m pese  más que otro que mida 1,20 m. Es más,  puede existir una relación aproximada entre ambas variables como la siguiente

 

A la deducción, a partir de una serie de datos, de este tipo de relaciones entre variables, es lo que se denomina  regresión.

 Figura 1.1: Mediante las técnicas de regresión de una variable   X  sobre una variable   Y  .,  se busca una función que sea una buena aproximación de una nube de puntos   (x_i , y_i )  ,mediante una curva del tipo

Para ello se asegurar que la  diferencia entre los valores    Y_i     e       sea tan pequeña como sea posible

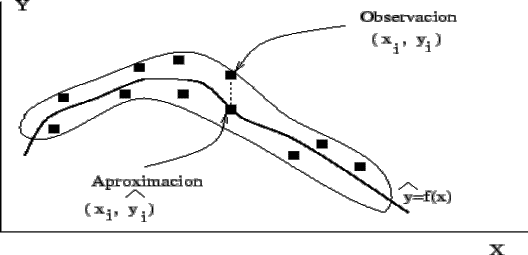Figura 1.1

Mediante las técnicas de regresión se propone una variable como función de otra variable X  (o viceversa),

 

Esto es lo que se denomina relación funcional. El criterio para construir  es que la diferencia entre    e    Y   sea pequeña.

El término que se denominado error debe ser tan pequeño como sea posible (figura 1.1). El objetivo será buscar la función (también denominada modelo de regresión)  que lo minimice. Véase la figura 1.2