a través
del tiempo con frecuencia está relacionada consigo misma, cuando se desfasa
uno o más periodos, a esta relación se le conoce como correlación entre ella
misma y en específico se le conoce como coeficiente de autocorrelación.Cuando se mide una variable
a través
del tiempo con frecuencia está relacionada consigo misma, cuando se desfasa
uno o más periodos, a esta relación se le conoce como correlación entre ella
misma y en específico se le conoce como coeficiente de autocorrelación.
Los patrones de datos que incluyen componentes como tendencia, estacionalidad, estacionaria e irregularidad se pueden estudiar usando el enfoque del análisis de autocorrelación. Los coeficientes de autocorrelación para diferentes desfases de tiempo de una variable se emplean para identificar patrones en las series de tiempo de datos
Con la siguiente ecuación se calcula los coeficientes de autocorrelación:
 |
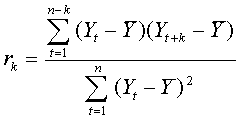en donde
rk , es el coeficiente de autocorrelación para un defasamiento de k periodos.
, es la media
de los valores de la serie
Yt , es la observación en el periodo de tiempo t
Yt+k , es la observación en k periodos posteriores o en el periodo t+k.
Por lo cual r1 es el coeficiente de autocorrelación en el primer defasamiento, r2 es el coeficiente de autocorrelación en el segundo defasamiento y así sucesivamente hasta un rk defasamiento.
Estacionalidad
Aleatoriedad
Tendencia
Estacionariedad
Una serie de datos será aleatoria si las autocorrelaciones r1,r2,......rk son cercanas estadísticamente a cero, como se presenta en la figura 1.6.
Figura 1.6 Correlograma de una serie de datos aleatoria*
 |
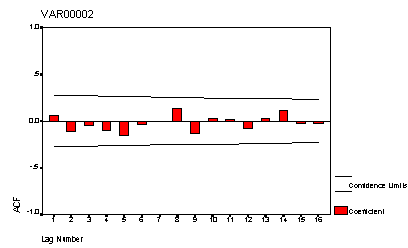*Gráfica elaborada mediante el paquete computacional SPSS
Tendencia Una serie de datos tendrá tendencia si r1 es cercana a 1 y las sucesivas r2,......rk caen lentamente a cero, como se presenta en la figura 1.7.
Figura 1.7 Correlograma de una serie de datos con tendencia*
 |
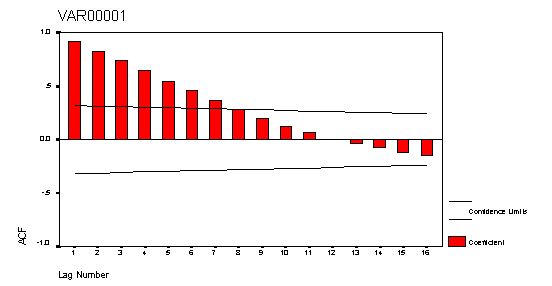*Gráfica elaborada mediante el paquete computacional SPSS
Estacional Una serie de datos tendrá un patrón estacional, cuando se presente un coeficiente de autocorrelación significativo en el periodo de defasamiento correspondiente; cuatro en los datos trimestrales o doce en los datos mensuales, como se presenta en la figura 1.8.
Figura 1.8 Correlograma de una serie de datos estacional
 |
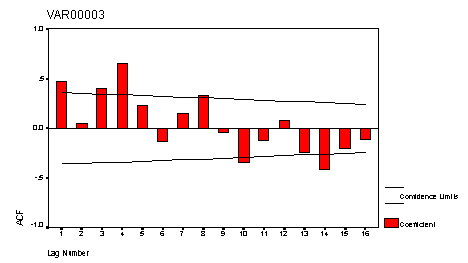*Gráfica elaborada mediante el paquete computacional SPSS
Estacionario Una serie de datos tendrá un patrón estacionario, cuando se presente un coeficiente de autocorrelación significativo en el primer periodo de defasamiento o en el periodo primer y segundo defasamiento correspondiente, como se presenta en la figura 1.9
Figura 1.9 Correlograma de una serie de datos estacionaria*
 |
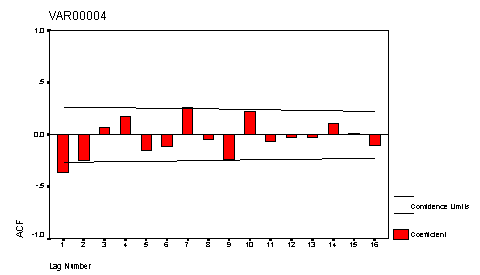*Gráfica elaborada mediante el paquete computacional SPSS
Una autocorrelación será significativa
o no según el criterio de Quenouille, que ha demostrado que los coeficientes
de autocorrelación de datos aleatorios tiene una distribución que se puede
aproximar a una curva normal con media cero y una desviación estándar de
.
Si una serie de datos en efecto corresponde a una serie de datos aleatorios, la mayoría de los coeficientes de autocorrelación debe ubicarse dentro del limite especificado por 0, o más o menos un cierto numero de errores estándar, un nivel específico de confianza, se puede considerar aleatoria una muestra, sí los coeficientes de autocorrelación calculados se encuentran dentro del intervalo, se dirá que los datos son aleatorios. El intervalo se construye a partir de la ecuación
 |
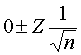en donde:
Z, es el valor normal estándar para un nivel de confianza dado
n, es el número de observaciones en la serie de datos
Un intervalo de confianza del 95 % se presenta en la siguiente desigualdad
 |
|
|
|
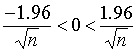Regresar |
